Chap.8 Stress due to Combined Loads
(조합하중에 의한 응력)
8.1 Introduction
1. Basic loading condition(기본 전재 조건)
- Axially loaded bar(축 하중을 받는 봉) : tension, compression, shear
- Shaft subjected to torque(비틀림을 받는 원형) : shear
- Bending of beams(보의 굽힘)
8.2 Thin-Walled Pressure Vessels(박벽 압력용기)
- Pressure vessel(압력용기)
: Internally or externally pressurized container, often cylindrical or spherical.(압력용기는 압력을 받는 원통형 또는 구형 용기입니다.)
- If the ratio r/t ≥10, the difference of stress between the inner and outer surfaces of the wall is less than 5%. Therefore, it can be assumed that stress is constant throughout its thickness. (r(반지름)/t(벽두께)≥10 이면, 벽의 내부와 외부사이의 응력은 5% 이하로 변합니다. 그래서 이런 응력들은 벽 두께에 걸쳐 거의 일정합니다.)
a. Cylindrical Vessels(원통형 용기)
- r(내부 반경), t(벽 두께), p(압력)
- σl : axial or longitudion al stress(축응력)
- σc : circumferential stress(원주응력)

(1) Circumferential stress, σc (원주응력)
원주응력은 자유물체도로부터 구할 수 있습니다. 이 자유물체도는 앞의 그림에 나타낸 미소길이 dx의 요소를 취하고, 직경을 따르는 평면을 반으로 절단해서 구해집니다.

resultant force due to the pressure acting on the diameter plane(지름면에 작용하는 압력에 의한 합력) : p(2rdx)
resultant force of circumferential stress(원주응력의 합력) 원통관의 벽에서 원주응력의 두께를 따라서 일정하다고 가정하면, 그 합력은 2(σctdx) 입니다.
유체의 무게를 무시한다면, 연직방향으로 힘의 평형은 다음과 같습니다.

이로부터 원주응력은 다음과 같습니다.

(2)Axial stress, σl (축방향 응력)
축방향 응력을 얻기 위해서는 단면을 따라 원통을 두 부분으로 절단해야합니다.

벽의 단면적은 다음과 같이 구해집니다.

용기의 평균 반경은 다음과 같이 구해집니다.

따라서 축방향 응력의 합력은 다음과 같이 구할 수 있습니다.
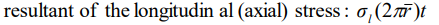
단면에 작용하는 압력의 합입니다.
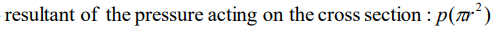
축력의 평형조건으로부터 다음을 얻을 수 있습니다.


- 원주응력과 축방향 응력을 비교하면, 원주응력이 축방향 응력의 두 배임을 알 수 있습니다. 이로인해 원통의 압력이 증가되어 파괴점에 이르면, 용기는 축방향선을 따라 쪼개지게 됩니다.
- 축방향 연결부의 강도는 둘레방향 연결부의 강도보다 두 배 크다는 것을 알 수 있습니다.
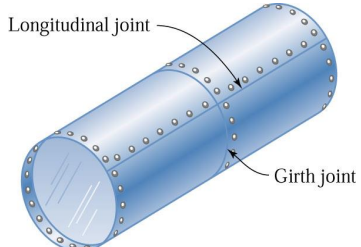
b. Spherical vessel(구형 용기)
- 원통에서 이용한 것과 유사한 해석을 사용하여 구형 박벽 압력용기의 벽에 작용하는 인장응력을 유도할 수 있습니다.
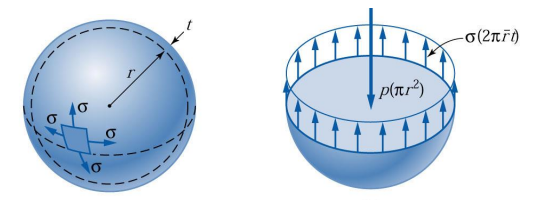
벽의 단면적에 대한 근사값은 다음과 같습니다.

유체의 원형 표면에서 작용하는 압력에 의한 합력은 다음과 같습니다.

아래의 평형방정식

으로부터 응력은 다음과 같습니다.
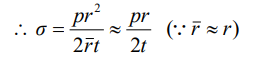
'전공공부' 카테고리의 다른 글
| Applied Mechanics of Materials(응용재료역학), 축하중과 횡하중의 조합 (0) | 2023.09.18 |
|---|---|
| 용접생산공학(1) (0) | 2023.09.17 |
| Stability of Floating Bodies(부유체안정론), 선체 기하학, 선체의 구조(명칭), 1week (1) | 2023.09.04 |

